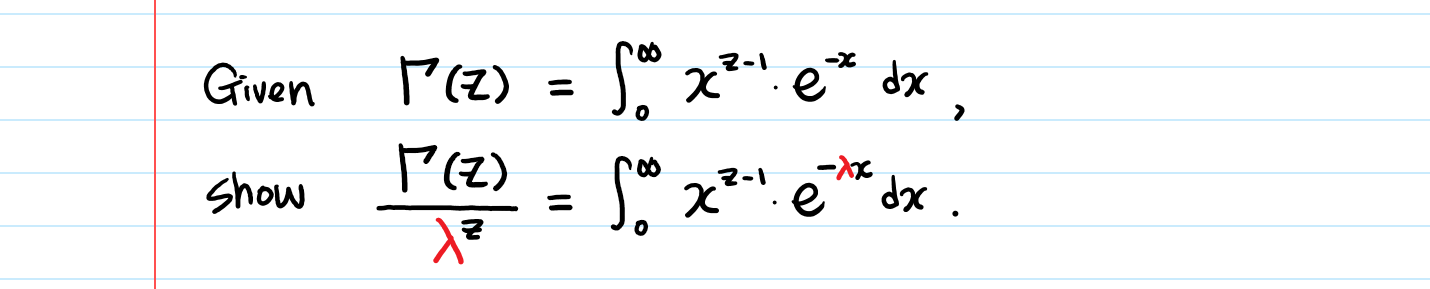Gamma Function Of 1 2 Proof

Making the substitution x u2 gives the equivalent expression 2 z 1 0 u2 1e u2du a special value of the gamma function can be derived when 2 1 0 1 2.

Gamma function of 1 2 proof. Table 2 contains the gamma function for arguments between 1 and 1 99. Using gamma function formula math gamma x 1 x gamma x math setting math x 1 2 math in above formula we get math gamma left 1 frac 1 2 right. First note that by definition of the gamma function. At the positive integer values for.

By elementary changes of variables this historical definition takes the more usual forms. Find a smooth curve that connects the points given by. The gamma function can be seen as a solution to the following interpolation problem. 4 the recursive relationship in 2 can be used to compute the value of the gamma function of all real numbers except the nonpositive integers by knowing only the value of the gamma function between 1 and 2.

This is mentioned as s. Let s take an example to understand the calculation of the gamma function in a better manner. Use respectively the changes of variable u log t and u2 log t in 1. Proof of 1 2 the gamma function is de ned as z 1 0 x 1e xdx.

A plot of the first few factorials makes clear that such a curve can be drawn but it would be preferable to have a formula that precisely describes the curve in which the number of operations does not. When 1 2 1 2 simpli es as 1 2 2 z 1 0 e u2du to derive the value for 1 2 the following steps are used. The gamma function evalated at 1 2 is 1 2 p ˇ. From this theorem we see that the gamma function γ x or the eulerian integral of the second kind is well defined and.

In the entry on the gamma function it is mentioned that γ 1 2 π in this entry we reduce the proof of this claim to the problem of computing the area under the bell curve. Gamma function formula example 1. Theorem 2 for x 0 γ x 0 tx 1e tdt 2 or sometimes γ x 20 t2x 1e t2dt. Assume if the number is a s and also it is a positive integer then the gamma function will be the factorial of the number.